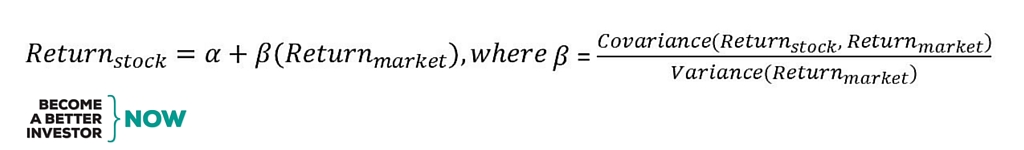Does High Risk Mean High Return?
Watch the video with Andrew Stotz or read the research below.
Let’s talk about beta
Remember that it’s calculated by regression. It indicates how much the return of the market and the stock move together. In one of the most used models, the Capital Asset Pricing Model (CAPM), beta is a measurement of risk. In theory, the higher the risk, the higher the expected rate of return.
A beta greater than 1.0x means that the stock moves in the same direction as the market but it’s more extreme; a beta of 1.0x means that a stock moves in line with the market; and a beta greater than zero but less than 1.0x means that the stock moves in the same direction as the market but less extreme.
Of course, a beta of zero means it’s uncorrelated to the market and a beta of less than zero means it moves in the opposite direction of the market which is very rare.
At A. Stotz Investment Research, our academic-style research format starts when we ask a research question. Then, we summarize previous research. Then, we formulate a hypothesis to test. After that, we select a relevant data set and remove errors and outliers; and we formulate a methodology to test the hypothesis.
From that, we present and analyze the results. Finally, we advise how to apply this result to improve investment decisions.
Question
- Does high risk mean high return?
- That is, will high-beta stocks yield a higher return than low-beta stocks? And what happens to beta over time?
- Is high or low beta sustained? If an analyst were to say, “this stock has a beta of 2.0x and that’s what I’m going to plug into the CAPM model,” does that make sense?
Review
Fletcher (2000) looked at the monthly international stock returns of MSCI equity indices of 18 developed markets between 1970 and 1998. It showed a significant positive relationship between beta and return in up markets and a significant negative relationship in down markets. This was not the case in January when there was a significant positive relationship in up markets but no relationship in down market months.
So the conclusion was that high beta stocks yielded high returns in up markets and high beta stocks performed worse in down markets.
Gençay et al. (2003) used daily returns for all stocks listed in the S&P 500 index between 1973 and 2000. From that, they constructed equally weighted portfolios each year. They measured the relationship between beta and return where beta was calculated at different “wavelet scales”: 2-4 days, 4-8 days, 8-16 days, 16-32 days, 32-64 days, and 65-128 days. The relation between beta (or risk) and return were more accurate at medium and long term; that would be 32-64 days and 64-128 days as compared to short time horizons which would be less than 32 days.
The conclusion was that high beta yielded high returns and vice versa, and that the relationship was stronger over longer time periods.
Huang and Hueng (2008) looked at time-varying beta to try to understand how that would work. They used daily returns of stocks included in the S&P 500 from 1987 to 2003; and calculated a time-varying beta using something they called “Adaptive Least Squares” instead of a constant beta. This was similar to a rolling beta and it aims to capture investors’ learning and their changes in expectations as a consequence.
What they found was a positive risk-return relationship that existed in up markets and a negative relationship in down markets. A time-varying beta gave a more accurate estimate of the per-unit risk price compared to a constant beta. So high beta yielded high returns in an up market.
In 2014, a research paper by Frazzini and Pedersen came out that was looking at betting against beta. This study looked at 20 companies across the world from 1925 to 2012 and international data from 1989 to 2012. They looked at both daily and monthly returns. Portfolios with high betas had lower excess returns and Sharpe ratios than portfolios with low betas.
A betting against beta factor portfolio, which was long leveraged low-beta assets and short high-beta assets, produced significant positive risk-adjusted returns. So here we find, different from the prior work, that betting against beta works.
Hypothesis 1
- Across the globe, high risk yields high return, i.e. investing in high-beta stocks should yield higher return than investing in low-beta stocks
Data
We looked at a global universe considering stocks with a market capitalization above US$100 million. That means we started with 58,000 stocks listed at any point in time on any stock exchange in the world from 1995 to 2015.
We excluded companies that had market capitalization lower than US$50 million dollars as of May 2015 which left us with about 27,000 companies. We also excluded 30% of the companies with the smallest market capitalizations each year from 1995 to 2015.
The minimum market cap included in any year ranged from US$29 million to US$169 million. On average, the minimum market cap over the 25 years was US$96 million.
Method
We calculated beta for each stock annually using weekly returns. At the end of each year, we calculated the beta of each stock relative to its local market index for that year. Beta is the slope of the coefficient of the regression in the CAPM model as you see here:
To eliminate outliers, data errors, and stocks with negative beta, we excluded stocks that had a beta less than or equal to zero or greater than 2.5x as stocks with a beta of zero or less were likely to be an error, inactive, or illiquid stocks. This excluded, on average, about 3.5% of the universe per year.
We further adjusted for outliers by cutting stocks that returned more than 500% or lost more than 80% in any one year. On average, this excluded about 0.7% of the universe each year. The objective was to get rid of errors in data and other very extreme outcomes that would not make the average representative. On average, we ended with about 10,000 companies per year.
We grouped the stocks in deciles from lowest to highest beta and constructed 10 portfolios, one from each decile. We held each portfolio for one year, re-ranked betas, and reformed new deciles at the end of that year and repeated this from December 1995 to December 2014. We then calculated the 20-year market-cap weighted return and standard deviation for each decile portfolio.
Results
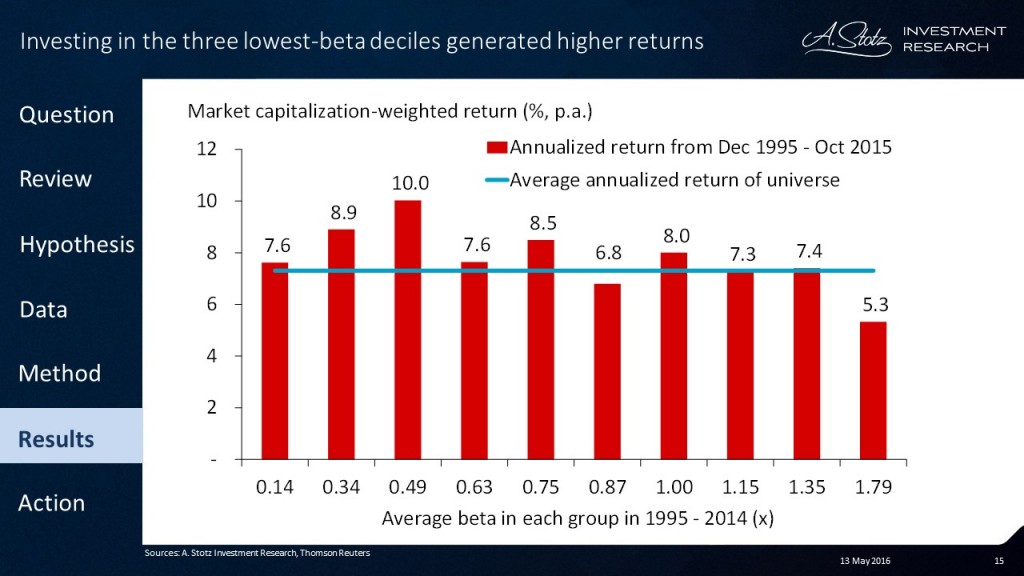
We found that investing in the three lowest beta deciles generated the highest return. Our analysis showed that the highest beta decile had an average beta of 1.79x and had an average annualized return of only 5.3%.
So one of the most definitive things we can see from this when we look at annualized return is that high beta does not equal high return.
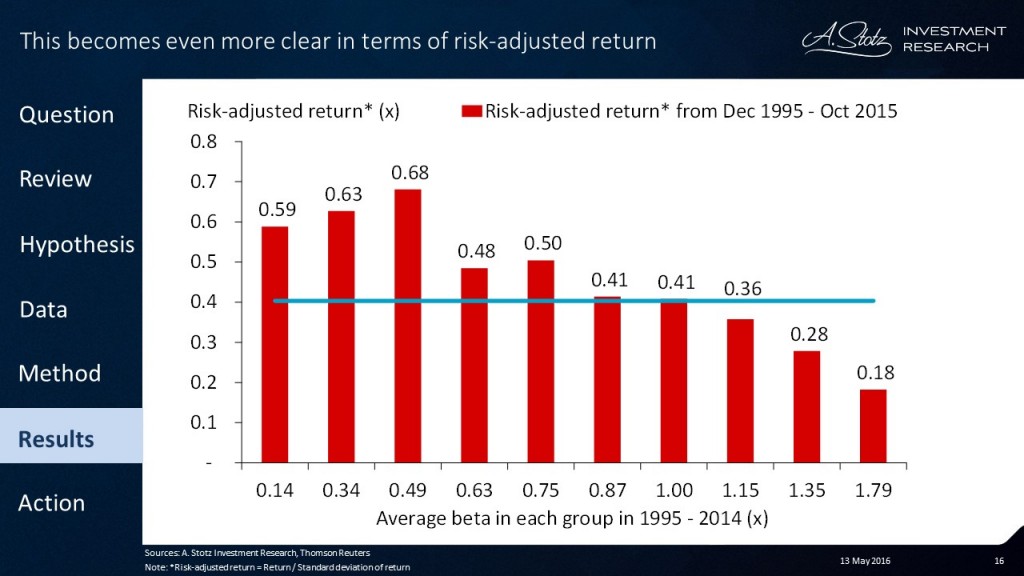
If we look at this on a risk-adjusted basis where we’re looking at the level of return relative to the risk that you’re bearing, we can see a much clearer relationship.
In fact, what we can see is that extremely low betas (that is anything from zero to 0.5x) tended to have a very high risk-adjusted return; and high betas (particularly 1.15x and above) tended to have a much lower risk-adjusted return.
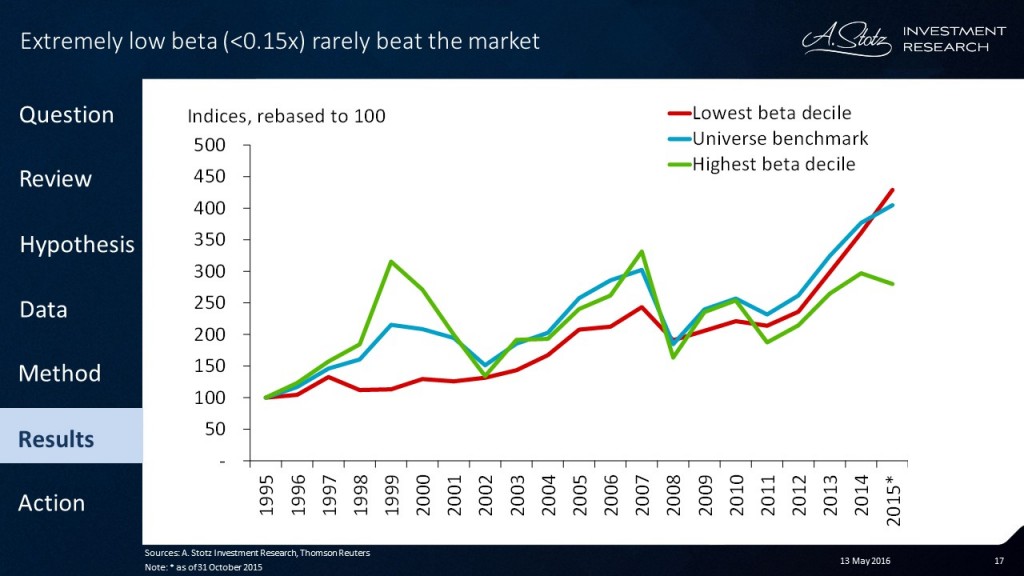
Looking at extreme betas (the most extreme decile, the lowest beta decile, and the highest beta decile) is not necessarily a good strategy.
Going for the most extremely low beta does not produce great performance; and going for the most extremely high beta, we can see, produces underperformance relative to the benchmark.
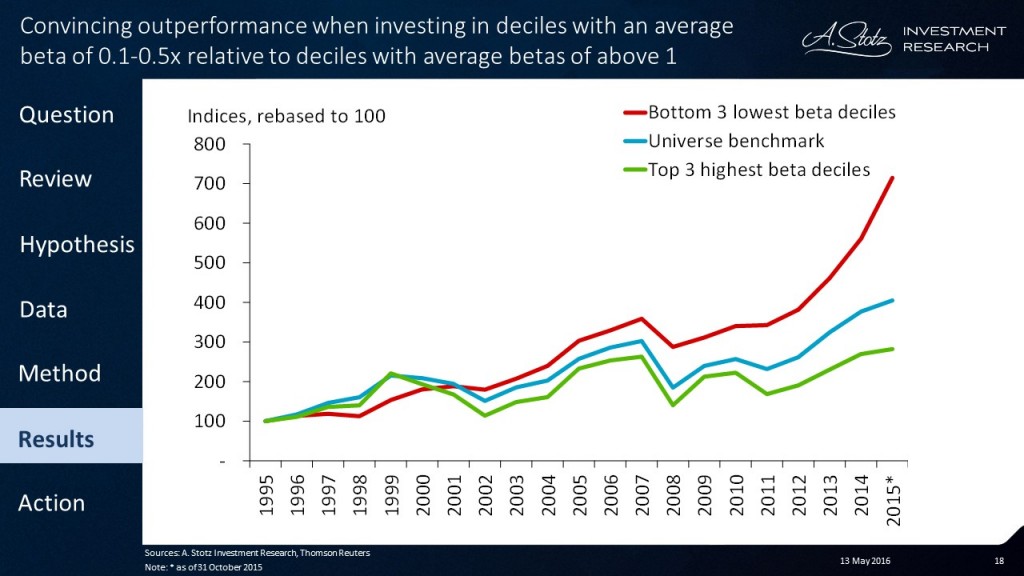
If we were to look at the bottom three lowest beta deciles and the top three highest beta deciles, we can see a significant outperformance for the low-beta portfolio and underperformance for the high-beta portfolio
In other words, low beta or what some people may call “low risk” equals high return.
Hypothesis 2
A second hypothesis that we wanted to test is that beta changes over time. Does it revert to 1.0x or does it stay where it is? If a company had a beta of 0.5x, would you want to use 0.5x in the forward forecast? If a company had a beta of 2.0x, would you use that in the forward forecast when trying to evaluate the value of a company in the CAPM model?
- Beta changes over time and reverts to 1
Results
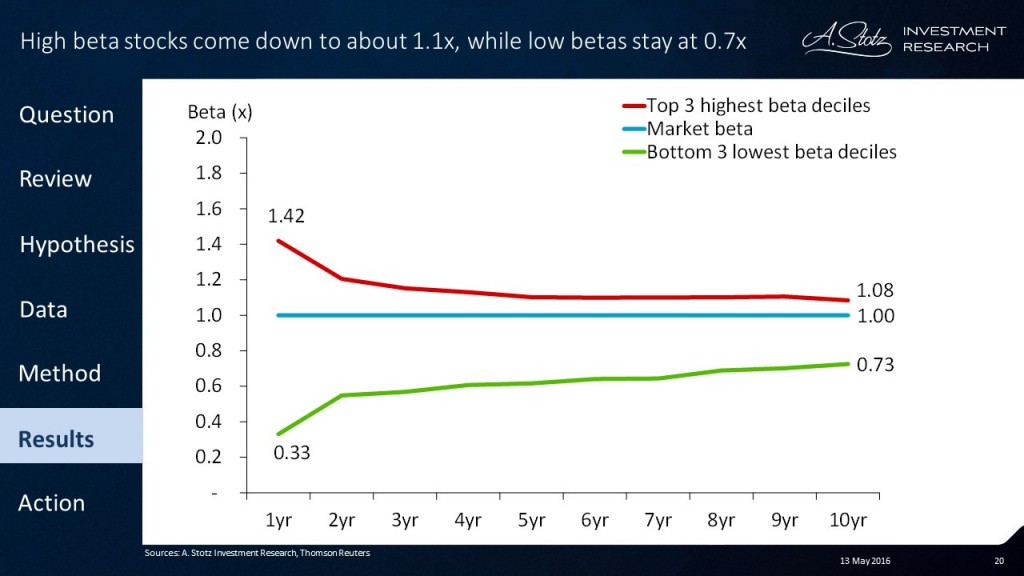
What we can see from our analysis is that you would not be right in doing that. In fact, if we look at the top three highest beta deciles and the bottom three lowest beta deciles, we can see that they start at 1.42x for the highest and 0.33x for the lowest; and they very quickly start reverting.
In the case of the highest beta, they revert to very close to 1.0x rather quickly. In the case of the lowest beta, they have a quick reversion initially, but then a very slow reversion that never gets to 1.0x. So particularly in the case of high-beta stocks, you definitely would not want to use whatever beta there is today for forward forecasting.
Action
- Investing in low-beta stocks generates higher returns, and it becomes more significant when it’s adjusted for risk
- Investing in the three deciles with the lowest average betas, between 0.1-0.5x, significantly beats the market
- Investing in the three deciles with the highest betas, on average betas of above 1.2x, significantly underperformed
- High risk ≠ high return
- High beta stocks revert to about 1.1x while low beta stocks tend to revert to about 0.7x
Do you think high #risk yields high #return? (assuming that beta=risk)
— Alexander Wetterling (@BkkBanker) May 13, 2016
Do you consider beta when investing in stocks? How do you use it? Do you look for high or low beta stocks? If you don’t consider beta, why not?
We’d love to hear from you in a comment below.
Feel free to share this article with your friends.
DISCLAIMER: This content is for information purposes only. It is not intended to be investment advice. Readers should not consider statements made by the author(s) as formal recommendations and should consult their financial advisor before making any investment decisions. While the information provided is believed to be accurate, it may include errors or inaccuracies. The author(s) cannot be held liable for any actions taken as a result of reading this article.